Нелинейная дискретная система представляет собой систему с линейной непрерывной частью первого порядка. Выходная переменная ЛНЧ с прямоугольными импульсами на входе в интервале очередного периода (см. Рис 33) описывается с учетом (5) и (7) разностным уравнением (9) при U=1:
; (9)
Замкнутая система первого порядка описывается нелинейным разностным уравнением первого порядка, которое состоит из разностного уравнения описывающего ЛНЧ (9), и уравнений замыкания, которые записываются в виде
где ym0- установившееся значение выходной переменной в конце импульса.
Исследование по линейному приближению разностных уравнений позволяют определить не только необходимые условия устойчивости, но и получить оценку быстродействия замкнутой схемы.
Линеаризуя разностные уравнения, описывающие замкнутую систему, в окрестности точки установившегося режима, получим:
, (10)
где l-корень характеристического уравнения. В системе с ШИМ-2 этот корень будет равен:
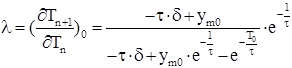, (11)
где d=1/к - тангенс угла наклона пилообразного сигнала( коэффициент усиления обратной связи), Т-длительность периода, Тn+1 и Тn -установившееся значение длительности импульса в n и n+1 периоды, t- постоянная времени цепи обратной связи.
Рассчитаем для данного дипломного проекта зависимость l от d=1/к для установившегося режима работы. Для этого определим постоянную времени t, которая равна отношению индуктивности рассчитанного дросселя к сопротивлению нагрузки:
, где Rн=Uн/Iн»1 Ом
(сопротивлением дросселя пренебрегаем), L=0.0002 Гн - индуктивность дросселя. В итоге получим постоянную времени t=4.
Для расчета l по формуле (11) введем исходные данные, которые переопределим в относительные единицы. Т=1 - длительность периода (Т=0.00005 сек), Т0/Т- относительная длительность импульса, t/Т=4 - относительная постоянная времени.
Подставляя эти значения в формулы (8) и (11) , и изменяя d от 0 до 0.3 определим l . Эта зависимость для t=4 и 10 при Т0/Т=0.2 и 0.8 приведена на рисунке. 34.
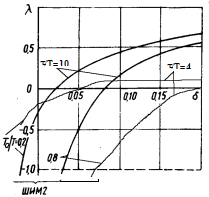
Рис. 34 Типовые корневые годографы системы с ШИМ-II при t/Т=4 и t/Т=10.
С уменьшением параметра d до корень уравнения l уменьшается до нуля, затем изменив знак увеличивается по абсолютному значению.
Исходя из уравнения (11) можно определить границы области устойчивости. Приравнивая формулу (11) к нулю получим оптимальное значение dопт, приравнивая к минус единице получим граничное значение dгр.
Рассмотрим подробнее:
1. Определение граничного коэффициента усиления (dгр=1/к).
Граничное значение определяется по формуле:
,
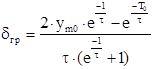введя относительные переменные найдем граничное значение которое при t/Т=4, Т0/Т=0.2, ymo=0.22 равно dгр=-0.085, при Т0/Т=0.2, ymo=0.819, dгр= 0.064, что соответствует коэффициентам усиления -11 и 15.
2. Определение оптимального коэффициента усиления (dопт=1/к).
Граничное значение определяется по формуле:
,
введя относительные переменные найдем граничное значение которое при t/Т=4, Т0/Т=0.2, ymo=0.22 равно dопт=0.055, при Т0/Т=0.8, ymo=0.819, dопт=0.205, что соответствует коэффициентам усиления 18 и 4.
Определение полной массы автомобиля
1.3 Определение нагрузки на колеса k1 = k2 = 0,5 - коэффициенты распределения массы по осям классического автомобиля. Подбор шин Для расчета выбираем шину 175/70 R13, где B = 175 мм - ширина профиля шины Н/В = 70% - соотношение высоты профиля шины к ширине мм - высота профиля шины мм - посадочный д ...
Параметры катушек добавочных полюсов
Средняя длина витка провода добавочных полюсов где bкд – ширина катушки добавочных полюсов, м; из чертежа полюсного окна принимаем bкд = 0,015 м. 2 · 0,245 + 3,14 · (0,018 + 0,015) = 0,594 м. Общая длина провода катушки , 0,594 · 29 = 17,23 м. Сопротивление меди катушек добавочных полюсов , Ом. ...
Выбор схем механизации
Схемой механизации называется графическое изображение комплекса перегрузочного оборудования и элементов материально-технической базы (подкрановые и железнодорожные пути, крытые и открытые склады, оперативные площадки), образующих грузовую линию для производства погрузо-разгрузочных работ. Для каждо ...
